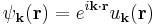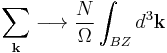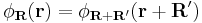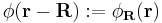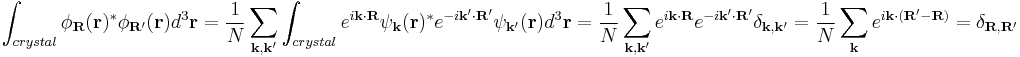Wannier function

The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier.[1][2]

The Wannier functions for different lattice sites in a crystal are orthogonal, allowing a convenient basis for the expansion of electron states in certain regimes. Wannier functions have found widespread use, for example, in the analysis of binding forces acting on electrons; they have proven to be in general localized, at least for insulators, in 2006.[3] Specifically, these functions are also used in the analysis of excitons and condensed Rydberg matter.

Contents

Definition

Although Wannier functions can be chosen in many different ways,[4] the original,[1] simplest, and most common definition in solid-state physics is as follows. Choose a single band in a perfect crystal, and denote its Bloch states by

\psi_{\mathbf{k}}(\mathbf{r}) = e^{i\mathbf{k}\cdot\mathbf{r}}u_{\mathbf{k}}(\mathbf{r})

where \, u_{\mathbf{k}}(\mathbf{r}) has the same periodicity as the crystal. Then the Wannier functions are defined by

\phi_{\mathbf{R}}(\mathbf{r}) = \frac{1}{\sqrt{N}} \sum_{\mathbf{k}} e^{-i\mathbf{k}\cdot\mathbf{R}} \psi_{\mathbf{k}}(\mathbf{r}),

where

\sum_{\mathbf{k}} \longrightarrow \frac{N}{\Omega} \int_{BZ} d^3\mathbf{k}

where "BZ" denotes the Brillouin zone, which has volume Ω.

Properties

On the basis of this definition, the following properties can be proven to hold:[5]

\phi_{\mathbf{R}}(\mathbf{r}) = \phi_{\mathbf{R}%2B\mathbf{R}'}(\mathbf{r}%2B\mathbf{R}')

In other words, a Wannier function only depends on the quantity (r-R). As a result, these functions are often written in the alternative notation

\phi(\mathbf{r}-\mathbf{R})�:= \phi_{\mathbf{R}}(\mathbf{r})
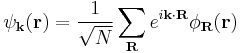\psi_{\mathbf{k}}(\mathbf{r}) = \frac{1}{\sqrt{N}} \sum_{\mathbf{R}} e^{i\mathbf{k}\cdot\mathbf{R}} \phi_{\mathbf{R}}(\mathbf{r}),

where the sum is over each lattice vector R in the crystal.

\int_{crystal} \phi_{\mathbf{R}}(\mathbf{r})^* \phi_{\mathbf{R'}}(\mathbf{r}) d^3\mathbf{r} = \frac{1}{N} \sum_{\mathbf{k,k'}}\int_{crystal} e^{i\mathbf{k}\cdot\mathbf{R}} \psi_{\mathbf{k}}(\mathbf{r})^* e^{-i\mathbf{k'}\cdot\mathbf{R'}} \psi_{\mathbf{k'}}(\mathbf{r}) d^3\mathbf{r} = \frac{1}{N} \sum_{\mathbf{k,k'}} e^{i\mathbf{k}\cdot\mathbf{R}} e^{-i\mathbf{k'}\cdot\mathbf{R'}} \delta_{\mathbf{k,k'}} = \frac{1}{N} \sum_{\mathbf{k}} e^{i\mathbf{k}\cdot\mathbf{(R'-R)}}=\delta_{\mathbf{R,R'}}

Wannier functions have been extended to nearly periodic potentials as well.[6]

Localization

The Bloch states 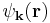\psi_{\mathbf{k}}(\mathbf{r}) are defined as the eigenfunctions of a particular Hamiltonian, and are therefore defined only up to an overall phase. By applying a phase transformation 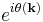e^{i\theta(\mathbf{k})} to the functions 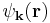\psi_{\mathbf{k}}(\mathbf{r}), for any (real) function 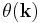\theta(\mathbf{k}), one arrives at an equally valid choice. While the change has no consequences for the properties of the Bloch states, the corresponding Wannier functions are significantly changed by this transformation.

One therefore uses the freedom to choose the phases of the Bloch states in order to give the most convenient set of Wannier functions. In practice, this is usually the maximally-localized set, in which the Wannier function \phi_{\mathbf{R}} is localized around the point R and rapidly goes to zero away from R. For the one-dimensional case, it has been proved by Kohn[7] that there is always a unique choice that gives these properties (subject to certain symmetries). This consequently applies to any separable potential in higher dimensions; the general conditions are not established, and are the subject of ongoing research.[3]

Modern theory of polarization

Wannier functions have recently found application in describing the polarization in crystals, for example, ferroelectrics. See for example, Berghold,[8] and Nakhmanson.,[9] and a power-point introduction by Vanderbilt[10] The polarization per unit cell in a solid can be defined as the dipole moment of the Wannier charge density:

\boldsymbol{p_c} = -e \sum_n \int\ d^3 r \,\, \boldsymbol r |W_n(\boldsymbol{r})|^2 \ ,

where the summation is over the occupied bands, and Wn is the Wannier function localized in the cell for band n. The change in polarization during a continuous physical process is the time derivative of the polarization and also can be formulated in terms of the Berry phase of the occupied Bloch states.[5][11]

References

  1. ^ a b "The structure of electronic excitation levels in insulating crystals," G. H. Wannier, Phys. Rev. 52, 191 (1937)
  2. ^ "Dynamics of Band Electrons in Electric and Magnetic Fields", G. H. Wannier, Rev. Mod. Phys. 34, 645 (1962)
  3. ^ a b Marzari et al.: Exponential localization of Wannier functions in insulators
  4. ^ Marzari et al.: An Introduction to Maximally-Localized Wannier Functions
  5. ^ a b A Bohm, A Mostafazadeh, H Koizumi, Q Niu and J Zqanziger (2003). The Geometric Phase in Quantum Systems. Springer. pp. §12.5, p. 292 ff. ISBN 3540000313. http://books.google.com/books?id=2XXWveovsRAC&pg=PA293&lpg=PA293&dq=berry++%22wannier+function%22#PPA292,M1. 
  6. ^ MP Geller and W Kohn Theory of generalized Wannier functions for nearly periodic potentials Physical Review B 48, 1993
  7. ^ W. Kohn, Analytic Properties of Bloch Waves and Wannier Functions, Phys. Rev. 115, 809 (1959)
  8. ^ Gerd Berghold et al. General and efficient algorithms for obtaining maximally localized Wannier functions
  9. ^ SM Nakhmanson et al. Spontaneous polarization and piezoelectricity in boron nitride nanotubes, 2008
  10. ^ D Vanderbilt Berry phases and Curvatures in Electronic Structure Theory.
  11. ^ C. Pisani (1994). Quantum-mechanical Ab-initio Calculation of the Properties of Crystalline Materials (Proceedings of the IV School of Computational Chemistry of the Italian Chemical Society ed.). Springer. p. 282. ISBN 3540616454. http://books.google.com/books?id=5ak5TwSLreAC&pg=PA282&dq=%22Berry+connection%22. 

Further reading

External links

See also